빅오(Big O) 표기법이란?

빅오 표기법

• 시간복잡도 : 컴퓨터가 계산하는 횟수
• 공간복잡도 : 변수가 차지하는 공간

빅오표기법을 활용한 여러 알고리즘을 공부해야하는 이유

-> 목적 : 결과만 같으면 되는가? 아니, 같은 문제에 대해 1시간이 걸릴수도 있고 30분이 걸릴 수도 있다. 이 점에 집중한다. 빅오를 이해하면 비효율적인 코드를 찾는 데 도움이 된다. 

 

좋은 코드는 빨라야하고, 메모리 사용이 적어야하고, 읽기 좋아야한다.

 

1. 속도는 (시간복잡성)

-> 기기 사양에 따라 다를 수있다. 같은 머신이어도 다른 시간이 걸릴 수 있다. 코드 시간만 측정하는 건 좋지 않다.

-> 컴퓨터가 해야하는 연산의 갯수가 중요하다? 2n 이든 5n+2든 정확한 숫자와는 사실 상관이 없다. 전체적인 추세가 중요하다.

 

2. 메모리 사용은? (공간복잡성)

-> 적을 수록 좋다.

 

3. 읽기 좋은가?

-> 짧고 읽기 좋은 것이 좋다.

 

 

시간복잡도

예시 1)

5n + 2개의 연상, n에 따라 실행시간이 올라간다.

그래서 시간 복잡도는 O(n)

function addUpto(n) {
    let total = 0;
    for(let i =1; i<= n; i++){
        total += i;
    }
    return total;
}

addUpto(3);

 

 

예시 2)

3개의 연산, 변화에 따라 실행시간은 변화하지 않는다.

그래서 시간복잡도는 O(1)

function addUpto(n) {
    return n * (n+1) /2;
}

addUpto(3);

 

 

예시 3)

for문이 중첩되어 있어 n에 따라 실행시간은 급격하게 올라간다.

그래서 시간복잡도는 O(n^2)

 

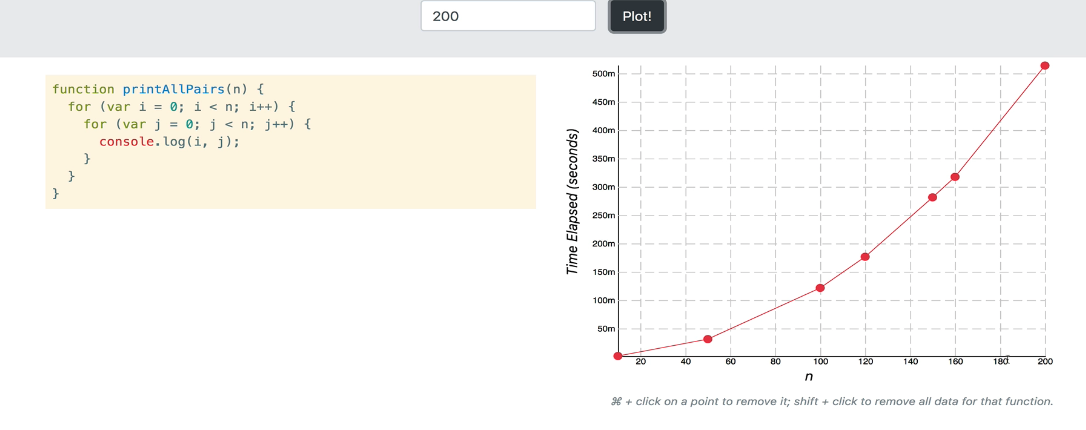
시간복잡도를 표현하는 방법은 궁극적으로 전체적으로 추세에 따라서 표기한다.

• O(2n) -> O(n) : 2n이나 n이나 n이 커질 수록 같은 형태의 시간복잡고 그래프 형태이다.
• O(500) -> O(1) : n에 따라 항상 똑같은 시간이 걸린다면 1로 표현한다.
• O(13n^2) -> O(n^2) : 그래프로 봤을 때, 13n^2이나 n^2 이나 추세 동일하다.
• O(n + 10) -> O(n) : n이 커질 수록 n + 10은 커지고 그래프로 봤을 때 10은 미미한 부분이라 n이라고만 표기한다.
• O(n^2 + 5n + 8) -> O(n제곱) : 전체적인 그래프로 봤을 때 5n + 8 미미한 부분이라 n^2이라고만 표기한다.

 

시간복잡도 구하기 연습문제

function logUpTo(n) {
    for (var i = 1; i <= n; i++) {
        console.log(i);
    }
}

-> O(n)

 

function logAtMost10(n) {
    for (var i = 1; i <= Math.min(n, 10); i++) {
        console.log(i);
    }
}

-> O(1)

 

 

function logAtLeast10(n) {
    for (var i = 1; i <= Math.max(n, 10); i++) {
        console.log(i);
    }
}

-> O(n)

 

function onlyElementsAtEvenIndex(array) {
    var newArray = Array(Math.ceil(array.length / 2));
    for (var i = 0; i < array.length; i++) {
        if (i % 2 === 0) {
            newArray[i / 2] = array[i];
        }
    }
    return newArray;
}

-> O(n)

 

function subtotals(array) {
    var subtotalArray = Array(array.length);
    for (var i = 0; i < array.length; i++) {
        var subtotal = 0;
        for (var j = 0; j <= i; j++) {
            subtotal += array[j];
        }
        subtotalArray[i] = subtotal;
    }
    return subtotalArray;
}

-> O(n^2)

 

 

공간복잡도

자바스크립트 기준을 봤을 때, 

• boolean, numbers, undefined, mull -> constant space : 일정한 공간을 차지한다.
• string  -> O(n) space : 문자열이 길어질 수록 공간을 많이 차지한다.
• object, array -> O(n) space : 길이가 길어질 수록 공간을 많이 차지한다.

 

예시 1)

total 과 i라는 변수가 공간을 차지하고 arr이 달라져도 똑같은 공간은 차지한다.

그래서 O(1)

예시 2)

arr의 길이에 따라 newArr의 길이가 길어지므로 arr의 길이에 따라 공간을 많이 차지하게 된다.

그래서  O(n)